RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 21. Areas of Bounded Regions

Subject: Maths - Class 12th

Q. No. 3 of Exercise 21.1

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

3

Find the area the region bounded by the parabola y2 = 4ax and the line x = a.

Given equations are:

x = a ...... (1)


And y2 = 4ax ...... (2)


Equation (1) represents a line parallel to the y - axis at a distance of units and equation (2) represents a parabola with vertex at origin and x - axis as its axis; A rough sketch is given as below: -


3.PNG


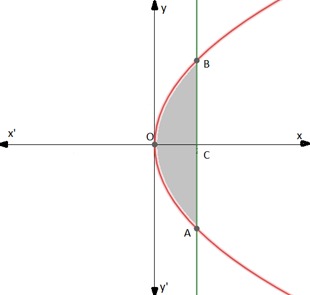
We have to find the area of the shaded region.


Required area


= shaded region OBAO


= 2 (shaded region OBCO) (as it is symmetrical about the x - axis)


(the area can be found by taking a small slice in each region of width Δx, then the area of that sliced part will be yΔx as it is a rectangle and then integrating it to get the area of the whole region)


(As x is between (0,a) and the value of y varies)


(as )



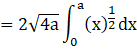
On integrating we get,




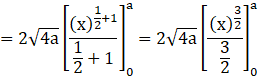
On applying the limits, we get,




Hence the area of the region bounded between the line x = a and the parabola y2 = 4ax is equal to square units.


Chapter Exercises

Exercise 21.2
Exercise 21.3
Exercise 21.4
Exercise 21.1
MCQ

More Exercise Questions

1

Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
2

Using integration, find the area of the region bounded by the line y – 1 = x, the x – axis and the ordinates x = – 2 and x = 3.
3

Find the area the region bounded by the parabola y2 = 4ax and the line x = a.
4

Find the area lying above the x - axis and under the parabola y = 4x – x2.
5

Draw a rough sketch to indicate the bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region
6

Make a rough sketch of the graph of the function y = 4 – x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x - axis and the lines x = 0 and x = 2.
7

Sketch the graph of in [0,4] and determine the area of the region enclosed by the curve, the x - axis and the lines x = 0, x = 4
8

Find the area under the curve above x - axis from x = 0 to x = 2. Draw a sketch of curve also.
9

Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2
10

Draw a rough sketch of the graph of the curve and evaluate the area of the region under the curve and above the x - axis
11

Sketch the region {(x,y):9x2 + 4y2 = 36} and the find the area of the region enclosed by it, using integration
12

Draw a rough sketch of the graph of the function y=2√1–x2,x[0,1] and evaluate the are enclosed between the curve and the x–axis.
13

Determine the area under the included between the lines x = 0 and x = 1
14

Using integration, find the area of the region bounded by the line 2y = 5x + 7, x - axis the lines x = 2 and x = 8.
15

Using definite integrals, find the area of circle x2 + y2 = a2
16

Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = - 2, x = 3, y = 0.
17

Sketch the graph y = |x - 5|. Evaluate . What does this value of the integral represent on the graph?
18

Sketch the graph y = |x + 3|. Evaluate . What does this integral represent on the graph?
19

Sketch the graph y = |x + 1|. Evaluate . What does the value of this integral represent on the graph?
20

Draw a rough sketch of the curve xy –3x – 2y – 10 = 0, x - axis and the lines x = 3, x = 4.
21

Draw a rough sketch of the curve and find the area between x - axis, the curve and the ordinates x = 0, x = π.
22

Draw a rough sketch of the curve and find the area between x - axis, the curve and the ordinates x = 0, x = π.
23

Find the area bounded by the curve y = cosx, x - axis and the ordinates x = 0 and x = 2π.
24

Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and are in the ration 2:3.
25

Compare the areas under the curves y = cos2x and y = sin2 x between x = 0 and x = π.
26

Find the area bounded by the ellipse and the ordinates x = ae and x = 0, where b2 = a2 (1 - e2) and e<1.
27

Find the area of the minor segment of the circle x2 + y2 = a2 cut off by the line .
28

Find the area of the region bounded by the curve x = at2, y = 2at between the ordinates corresponding t = 1 and t = 2
29

Find the area enclosed by the curve x = 3 cost, y = 2 sint

Students Store