RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 21. Areas of Bounded Regions

Subject: Maths - Class 12th

Q. No. 28 of Exercise 21.1

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

28

Find the area of the region bounded by the curve x = at2, y = 2at between the ordinates corresponding t = 1 and t = 2

Given equations are:

x = at2 ...... (1)


y = 2at ..... (2)


t = 1 ..... (3)


t = 2 ..... (4)


Equation (1) and (2) represents the parametric equation of the parabola.


Eliminating the parameter t, we get



This represents the Cartesian equation of the parabola opening towards the positive x - axis with focus at (a,0).


A rough sketch of the circle is given below: -


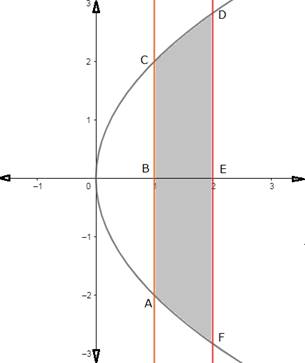
28.PNG


When t = 1, x = a


When t = 2, x = 4a


We have to find the area of shaded region.


Required area


= (shaded region ABCDEF)


= 2(shaded region BCDEB)


(the area can be found by taking a small slice in each region of width Δx, then the area of that sliced part will be yΔx as it is a rectangle and then integrating it to get the area of the whole region)


(As x is between and the value of y varies, here y is Cartesian equation of the parabola)


(as )



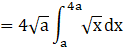
On integrating we get,


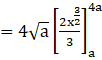(by applying power rule)


On applying the limits we get,





Hence the area of the region bounded by the curve x = at2, y = 2at between the ordinates corresponding t = 1 and t = 2 is equal to square units.


Chapter Exercises

Exercise 21.2
Exercise 21.3
Exercise 21.4
Exercise 21.1
MCQ

More Exercise Questions

1

Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
2

Using integration, find the area of the region bounded by the line y – 1 = x, the x – axis and the ordinates x = – 2 and x = 3.
3

Find the area the region bounded by the parabola y2 = 4ax and the line x = a.
4

Find the area lying above the x - axis and under the parabola y = 4x – x2.
5

Draw a rough sketch to indicate the bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region
6

Make a rough sketch of the graph of the function y = 4 – x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x - axis and the lines x = 0 and x = 2.
7

Sketch the graph of in [0,4] and determine the area of the region enclosed by the curve, the x - axis and the lines x = 0, x = 4
8

Find the area under the curve above x - axis from x = 0 to x = 2. Draw a sketch of curve also.
9

Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2
10

Draw a rough sketch of the graph of the curve and evaluate the area of the region under the curve and above the x - axis
11

Sketch the region {(x,y):9x2 + 4y2 = 36} and the find the area of the region enclosed by it, using integration
12

Draw a rough sketch of the graph of the function y=2√1–x2,x[0,1] and evaluate the are enclosed between the curve and the x–axis.
13

Determine the area under the included between the lines x = 0 and x = 1
14

Using integration, find the area of the region bounded by the line 2y = 5x + 7, x - axis the lines x = 2 and x = 8.
15

Using definite integrals, find the area of circle x2 + y2 = a2
16

Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = - 2, x = 3, y = 0.
17

Sketch the graph y = |x - 5|. Evaluate . What does this value of the integral represent on the graph?
18

Sketch the graph y = |x + 3|. Evaluate . What does this integral represent on the graph?
19

Sketch the graph y = |x + 1|. Evaluate . What does the value of this integral represent on the graph?
20

Draw a rough sketch of the curve xy –3x – 2y – 10 = 0, x - axis and the lines x = 3, x = 4.
21

Draw a rough sketch of the curve and find the area between x - axis, the curve and the ordinates x = 0, x = π.
22

Draw a rough sketch of the curve and find the area between x - axis, the curve and the ordinates x = 0, x = π.
23

Find the area bounded by the curve y = cosx, x - axis and the ordinates x = 0 and x = 2π.
24

Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and are in the ration 2:3.
25

Compare the areas under the curves y = cos2x and y = sin2 x between x = 0 and x = π.
26

Find the area bounded by the ellipse and the ordinates x = ae and x = 0, where b2 = a2 (1 - e2) and e<1.
27

Find the area of the minor segment of the circle x2 + y2 = a2 cut off by the line .
28

Find the area of the region bounded by the curve x = at2, y = 2at between the ordinates corresponding t = 1 and t = 2
29

Find the area enclosed by the curve x = 3 cost, y = 2 sint

Students Store