A manufacturer has three machines installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table :
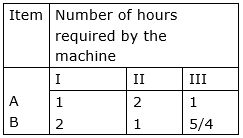
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produce to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
Let x units of item A and y units of item B be manufactured. Therefore, x, y 
0.
As we are given,
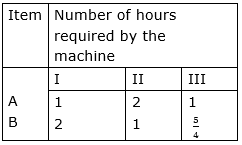
Machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day.
According to the question, the constraints are
x + 2y 
12
2x + y 
12
x + 
y 
5
He makes a profit of Rs 6.00 on item A and Rs. 4.00 on item B. Profit made by him in producing x items of A and y items of B is 6x + 4y.
Total profit Z = 6x + 4y which is to be maximized
Thus, the mathematical formulation of the given linear programming problem is
Max Z = 6x + 4y, subject to
x + 2y 
12
2x + y 
12
x + 
y 
5
x, y 
0
First, we will convert the inequations into equations as follows:
x + 2y = 12, 2x + y = 12, x + 
y = 5, x = 0 and y = 0.
The region represented by x + 2y 
12
The line x + 2y = 12 meets the coordinate axes at A(12,0) and B(0,6) respectively. By joining these points, we obtain the line x + y = 12. Clearly (0, 0) satisfies the x + 2y = 12. So, the region which contains the origin represents the solution set of the inequation x + 2y 
12
The region represented by 2x + y 
12
The line 2x + y = 12 meets the coordinate axes at C(6,0) and D(0,12) respectively. By joining these points, we obtain the line 2x + y = 12. Clearly (0, 0) satisfies the 2x + y = 12. So, the region which contains the origin represents the solution set of the inequation 2x + y 
12
The region represented by x + 
y 
5
The line x + 
y 
5 meets the coordinate axes at E(5,0) and F(0,4) respectively. By joining these points, we obtain the line x + 
y = 5. Clearly (0, 0) satisfies the x + 
y 
5. So, the region which does not contain the origin represents the solution set of the inequation x + 
y 
5
The region represented by x 
0, y 
0 :
Since every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x 
0 and y 
0.
The feasible region determined by the system of constraints
x + 2y 
12, 2x + y 
12, x + 
y 
5, x, y 
0 are as follows.
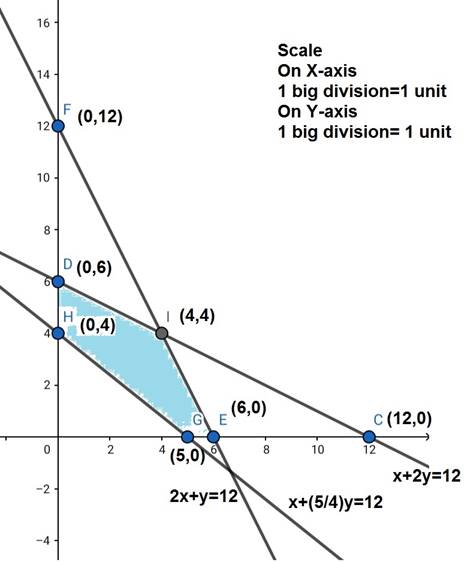
Thus the maximum profit is of Rs 40 obtained when 4 units each of item A and B are manufactured.
The corner points are D(0,6), I(4,4), C(6,0), G(5,0), and H(0,4). The values of Z at these corner points are as follows:
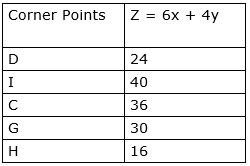
The maximum value of Z is 40 which is attained at I(4, 4).