Let tailor A work for x days and tailor B work for y days.

In one day, A can stitch 6 shirts and 4 pants whereas B can stitch 10 shirts and 4 pants.

Thus in x days, A can stitch 6x shirts and 4x pants whereas in y days B can stitch 10y shirts and 4y pants.

It is given that the minimum requirement of the shirt and pants are respectively 60 and 32.

Thus,

6x + 10y 60

4x + 4y 32

Further it is given that A and B earn Rs 15 and Rs 20 per day respectively. Thus, A earn Rs 15x and B earns Rs 20y.

Let Z denotes the total cost

Z = 15x + 20y

Days cannot be negative.

x,y 0.

MIN Z = 15x + 20y

Subject to

6x + 10y 60

4x + 4y 32

x,y 0

First we will convert inequations into equations as follows:

6x + 10y = 60, 4x + 4y = 32, x = 0, y = 0

Region represented by 6x + 10y 60

The line 6x + 10y = 60 meets the coordinate axes at A(10,0) and B(0,6) respectively. By joining these points we obtain the line 6x + 10y = 60. Clearly (0, 0) satisfies the 6x + 10y 60. So, the region which does not contains the origin represents the solution set of the inequation 6x + 10y 60

Region represented by 4x + 4y 32

The line 4x + 4y = 32 meets the coordinate axes at C(8,0) and D(0,8) respectively. By joining these points we obtain the line 4x + 4y = 32. Clearly (0, 0) satisfies the 4x + 4y 32. So, the region which does not contains the origin represents the solution set of the inequation 4x + 4y 32.

Region represented by x 0, y 0 :

Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x 0 and y 0.

The feasible region determined by the system of constraints 6x + 10y 60, 4x + 4y 32

x,y 0 are as follows.

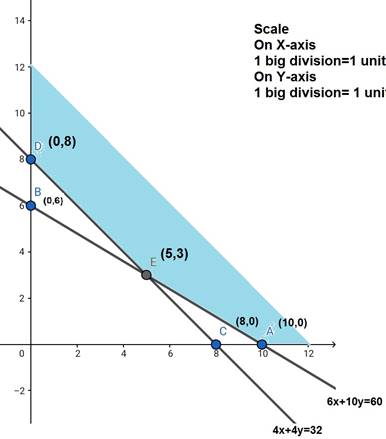
The corner points are D(0,8), E(5,3), A(10,00. The values of Z at these corner points are as follows:

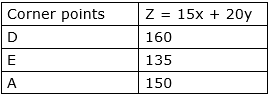
The minimum value of Z is 135 which is attained at E(5,3).

Thus, for minimum labour cost, A should work for 5 days and B should work for 3 days.