Let the company produces x belts of types A and y belts of type B. Number of belts cannot be negative. Therefore, x,y 0.

It is given that leather is sufficient only for 800 belts per day (both A and B combined).

Therefore,

x + y 800

It is given that the rate of production of belts of type B is 1000 per day. Hence the time taken to produce y belts of type B is .

And, since each belt of type A requires twice as much time as a belt of type B, the rate of production of belts of type A is 500 per day and therefore, total time taken to produce x belts of type A is

Thus, we have,

Or, 2x + y 1000

Belt A requires fancy buckle and only 400 fancy buckles are available for this per day.

x 400

For Belt of type B only 700 buckles are available per day.

y 700

profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Therefore, profit gained on x belts of type A and y belts of type B is Rs 2x and Rs 1.50y respectively. Hence, the total profit would be Rs(2x + 1.50y). Let Z denote the total profit

Z = 2x + 1.50y

Thus, the mathematical formulation of the given linear programming problem is;

Max Z = 2x + 1.50y subject to

x + y 800

2x + y 1000

x 400

y 700

First we will convert these inequations into equations as follows:

x + y = 800

2x + y = 1000

x = 400

y = 700

Region represented by x + y = 800

The line x + y = 800 meets the coordinate axes at A(800,0) and B(0,800) respectively. By joining these points we obtain the line x + y = 800. Clearly (0, 0) satisfies the x + y 800. So, the region which contains the origin represents the solution set of the inequation x + y 800.

Region represented by 2x + y 1000

The line 2x + y = 1000 meets the coordinate axes at C(500,0) and D(0,1000) respectively. By joining these points we obtain the line 2x + y = 1000. Clearly (0, 0) satisfies the 2x + y 1000. So, the region which contains the origin represents the solution set of the inequation 2x + y 1000.

Region represented by x 400

The line x = 400 will pass through (400,0). The region to the left of the line x = 400 will satisfy the inequation x 400

Region represented by y 700

The line y = 700 will pass through (0,700). The region to the left of the line y = 700

will satisfy the inequation y 700.

Region represented by x 0, y 0 :

Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x 0 and y 0.

The feasible region determined by the system of constraints x + y 800, 2x + y 1000, x 400,

y 700

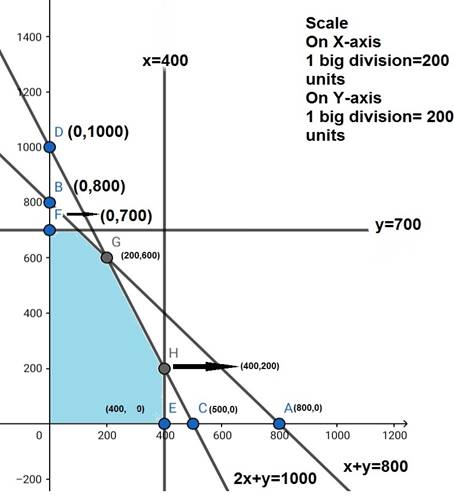
The corner points are F(0,700), G(200,600), H(400,200), E(400,0). The values of Z at these corner points are as follows

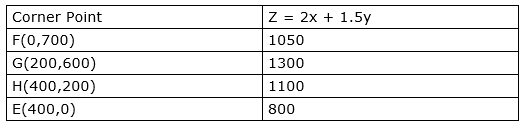
The maximum value of Z is 1300 which is attained at G(200,600).

Thus, the maximum profit obtained is Rs 1300 when 200 belts of type A and 600 belts of type B are produced.