A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?

Let required number of goods A and B are x and y respectively.


Since, profits of each A and B are Rs. 40 and Rs. 50 respectively. So, profits on x number of type A and y number of type B are 40x and 50y respectively.


Let Z denotes total output daily, so,


Z = 40x + 50y


Since, each A and B requires 3 grams and 1 gram of silver respectively. So, x of type A and y of type B require 3x and y of silver respectively. But,


Total silver available is 9 grams. So,


3x + y 9 {First Constraint}


Since each A and B requires 1 gram and 2 grams of gold respectively. So, x of type A and y of type B require x and 2y respectively.


But total gold available is 8 grams.


So,


x + 2y 8 {Second Constraint}


Hence mathematical formulation of the given LPP is,


Max Z = 40x + 50y


Subject to constraints,


3x + y 9


x + 2y 8


x,y 0 [Since production of A and B can not be less than zero]


Region 3x + y 9: line 3x + y = 9 meets the axes at A(3,0), B(0,9) respectively.


Region containing the origin represents 3x + y 9


as origin satisfies 3x + y 9.


Region x + 2y 8: line x + 2y = 8 meets the axes at C(8,0), D(0,4) respectively.


Region containing the origin represents x + 2y 8 as origin satisfies x + 2y 8.


Region x,y 0: it represents the first quadrant.


9.jpg


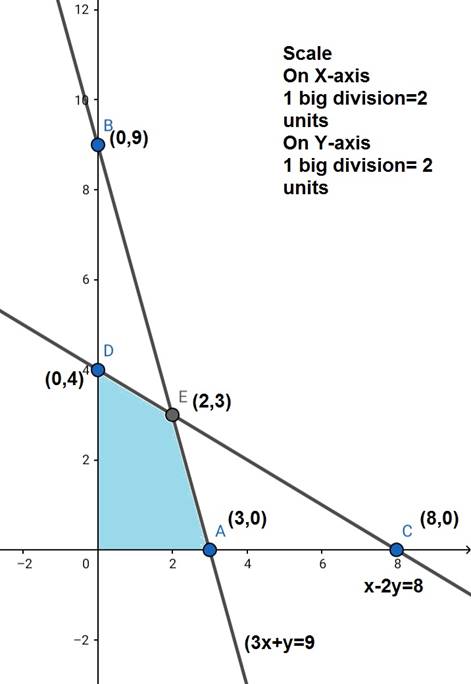
The corner points are O(0,0), D(0,4), E(2,3), A(3,0)


The values of Z at these corner points are as follows



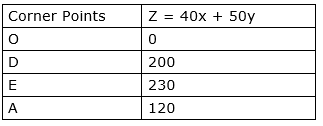
The maximum value of Z is 230 which is attained at E(2,3).


Thus the maximum profit is of Rs 230 when 2 units of Type A 3 uniits of Type B are produced.


9