A firm manufacturing two type of electric items, A and B, can make a profit of 20 per unit of A and ₹ 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programming problem for maximum profit and solve it graphically.
Let x units of item A and y units of item B were manufactured.
Numbers of items cannot be negative. Therefore,
x, y 
0
The given information can be tabulated as follows:
Further, it is given that type B is an export model, whose supply is restricted to 65 units per month.
Therefore, the constraints are
3x + 2y 
210
4x + 4y 
300
y 
65
A and B can make profit of Rs 20 and Rs 30 per unit respectively.
Therefore, profit gained from x units of item A and y units of item B is Rs 20x and 30y respectively.
Total Profit = Z = 20x + 30y which according to question is to be maximised.
Thus the mathematical formulation of the given LPP is,
Max Z = 20x + 30y
Subject to constraints
3x + 2y 
210
4x + 4y 
300
y 
65
x, y 
0
Region represented by 3x + 2y 
210: The line 3x + 2y = 210 meets the axes at A(70,0), B(0,105) respectively.
Region containing the origin represents 3x + 2y 
210 as origin satisfies 3x + 2y 
210.
Region represented by 4x + 4y 
300: The line 4x + 4y = 300 meets the axes at C(75,0), D(0,75) respectively.
Region containing the origin represents 4x + 4y 
300 as origin satisfies 4x + 4y 
300
y = 65 is the line passing through the point E(0,65) and is parallel to X - axis.
Region x,y 
0: it represents the first quadrant.
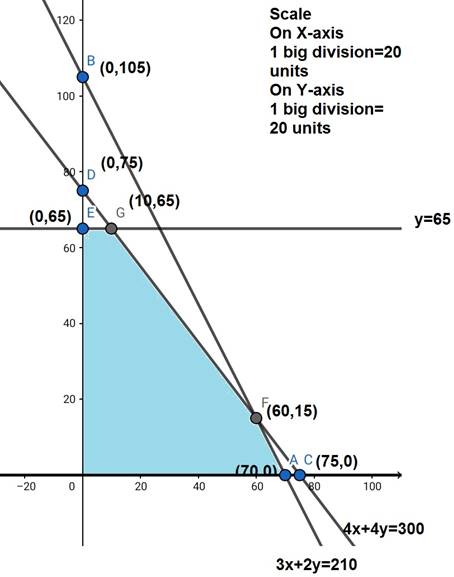
The corner points are O(0,0), E(0,65), G(10,65), F(60,15) and A(70,0).
The values of Z at these corner points are as follows:
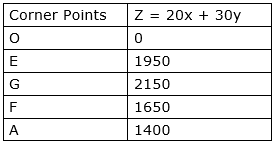
The maximum value of Z is 2150 which is attained at G(10,65).
Thus, the maximum profit is Rs. 2150 obtained when 10 units of item A and 65 units of item B are manufactured.