A factory uses three different resources for the manufacture of two different products,20 units of the resources a, 12 units of B and 16 units of C being available 1 unit of the first product requires 2,2 and 4 units of the respective resources and 1 unit of the second product requires 4,2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
Let number of product I and product II are x and y respectively.
Since, profits on each product I and II are 2 and 3 monetary unit. So, profits on x number of Product I and y number of Product II are 2x and 3y respectively.
Let Z denotes total output daily, so,
Z = 2x + 3y
Since, each I and II requires 2 and 4 units of resources A. So, x units of product I and y units of product II requires 2x and 4y minutes respectively. But, maximum available quantity of resources A is 20 units.
So,
2x + 4y ![]() 20
20
x + 2y ![]() 10 {First Constraint}
10 {First Constraint}
Since, each I and II requires 2 and 2 units of resources B. So, x units of product I and y units of product II requires 2x and 2y minutes respectively. But, maximum available quantity of resources A is 12 units.
So,
2x + 2y ![]() 12
12
x + y ![]() 6 {Second Constraint}
6 {Second Constraint}
Since, each units of product I requires 4 units of resources C. It is not required by product II. So, x units of product I require 4x units of resource C. But, maximum available quantity of resources C is 16 units.
So,
4x ![]() 16
16
x ![]() 4 {Third Constraint}
4 {Third Constraint}
Hence mathematical formulation of LPP is,
Max Z = 2x + 3y
Subject to constraints,
x + 2y ![]() 10
10
x + y ![]() 6
6
x ![]() 4
4
x, y ![]() 0 [ Since production for I and II can not be less than zero]
0 [ Since production for I and II can not be less than zero]
Region represented by x + 2y ![]() 10: The line x + 2y = 10 meets the axes at A(10,0), B(0,5) respectively.
10: The line x + 2y = 10 meets the axes at A(10,0), B(0,5) respectively.
Region containing the origin represents x + 2y ![]() 10 as origin satisfies x + 2y
10 as origin satisfies x + 2y ![]() 10.
10.
Region represented by x + y ![]() 6: The line x + y = 6 meets the axes at C(6,0), D(0,6) respectively. Region containing the origin represents x + y
6: The line x + y = 6 meets the axes at C(6,0), D(0,6) respectively. Region containing the origin represents x + y ![]() 6 as origin satisfies x + y
6 as origin satisfies x + y ![]() 6
6
Region x,y ![]() 0: it represents the first quadrant.
0: it represents the first quadrant.
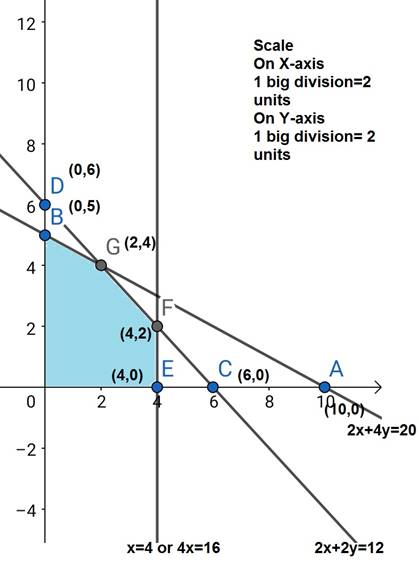
The corner points are O(0,0), B(0,5), G(2,4), F(4,2), and E(4,0).
The values of Z at these corner points are as follows:
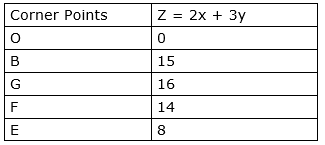
The maximum value of Z is 16 which is attained at G (12,4).
Thus, the maximum profit is 16 monetary units obtained when 2 units of first product and 4 units of second product were manufactured.