The given system can be written in matrix form as:

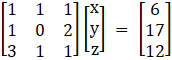
A X = B

Now, |A| = 1

= 1(– 2) – 1(1 – 6) + 1(1)

= – 2 + 5 + 1

= 4

So, the above system has a unique solution, given by

X = A ^{– 1}B

Cofactors of A are:

C₁₁ = (– 1)^{1 + 1} 0 – 2 = – 2

C₂₁ = (– 1)^{2 + 1} 1 – 1 = 0

C₃₁ = (– 1)^{3 + 1} 2 – 0 = 2

C₁₂ = (– 1)^{1 + 2} 1 – 6 = 5

C₂₂ = (– 1)^{2 + 1} 1 – 3 = – 2

C₃₂ = (– 1)^{3 + 1} 2 – 1 = – 1

C₁₃ = (– 1)^{1 + 2} 1 – 0 = 1

C₂₃ = (– 1)^{2 + 1} 1 – 3 = 2

C₃₃ = (– 1)^{3 + 1} 0 – 1 = – 1

adj A =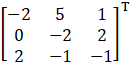

=

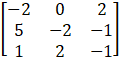
A ^{– 1} =

Now, X = A ^{– 1}B =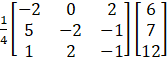

X =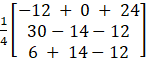

X =

X =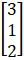

Hence, X = 3,Y = 1 and Z = 2