When a die is thrown 3 times, total possible outcomes are, 6³ = 216

A= 4 appears on third toss =

{(1,1,4),(1,2,4),(1,3,4),(1,4,4),(1,5,4),(1,6,4)

(2,1,4),(2,2,4),(2,3,4),(2,4,4),(2,5,4),(2,6,4)

(3,1,4),(3,2,4),(3,3,4),(3,4,4),(3,5,4),(3,6,4)

(4,1,4), (4,2,4)(4,3,4),(4,4,4),(4,5,4),(4,6,4)

(5,1,4),(5,2,4),(5,3,4)(5,4,4),(5,5,4),(5,6,4)

(6,1,4),(6,2,4),(6,3,4),(6,4,4),(6,5,4),(6,6,4)}

=36

Hence P(A) =

B= 6,5 appears respectively on first two tosses

{(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6)}

= 6

Hence P(B) =

(A ∩ B) = 6,5 occurs on first two toss and 4 occur on third toss = (6,5,4) = 1

P (A ∩ B) =

Hence =

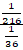= = (answer)

= (answer)