The bag A contains 8 white and 7 black balls while the bag B contains 5 white and 4 black balls. One balls is randomly picked up from the bag A and mixed up with the balls in bag B. Then a ball is randomly drawn out from it. Find the probability that ball drawn is white.
Given:
Bag A contains 8 white and 7 black balls.
Bag B contains 5 white and 4 black balls.
A ball is transferred from bag A to bag B and then a ball is drawn from bag B.
There are two mutually exclusive ways to draw a white ball from bag B –
a. A white ball is transferred from bag A to bag B, and then, a white ball is drawn from bag B
b. A black ball is transferred from bag A to bag B, and then, a white ball is drawn from bag B
Let E1 be the event that white ball is drawn from bag A and E2 be the event that black ball is drawn from bag A.
Now, we have
![]()
![]()
![]()
We also have
![]()
![]()
![]()
Let E3 denote the event that white ball is drawn from bag B.
Hence, we have
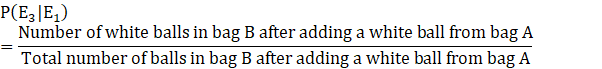
![]()
![]()
We also have
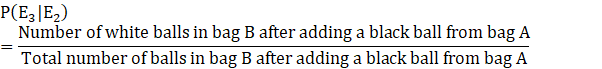
![]()
![]()
Using the theorem of total probability, we get
P(E3) = P(E1)P(E3|E1) + P(E2)P(E3|E2)
![]()
![]()
![]()
Thus, the probability of the drawn ball being white is![]() .
.