In a binomial distribution, the sum and product of the mean and the variance are 25/3 and 50/3 respectively. Find the distribution.

Question

Philoid · Accepted Answer

Let n and p be the parameters of the required binomial distribution. So,

1 - p = q

Also,

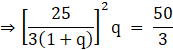
⇒625q = 150[(1+q)²]

⇒25q = 6[(1+q)²]

⇒6 + 6q² + 12q – 25q = 0

⇒6q² – 13q + 6 = 0

⇒6q² – 9q - 4q + 6 = 0

⇒3q(2q - 3) - 2(2q - 3) = 0

⇒(2q - 3)(3q - 2) = 0

⇒(2q - 3) = 0 or (3q - 2) = 0

As, q≤1

Now, p = 1 - q

⇒n = 15

The required binomial distribution is given by,