Given the height of a cone increases by k%.

Let x be the height of the cone and Δx be the change in the value of x.

Hence, we have

∴ Δx = 0.01kx

Let us assume the radius, the slant height and the semi-vertical angle of the cone to be r, l and α respectively as shown in the figure below.

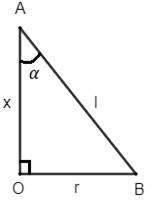
From the above figure, using trigonometry, we have

∴ r = x tan(α)

We also have

∴ l = x sec(α)

(i) The total surface area of the cone is given by

S = πr² + πrl

From above, we have r = x tan(α) and l = x sec(α).

⇒ S = π(x tan(α))² + π(x tan(α))(x sec(α))

⇒ S = πx²tan²α + πx²tan(α)sec(α)

⇒ S = πx²tan(α)[tan(α) + sec(α)]

On differentiating S with respect to x, we get

We know

Recall that if y = f(x) and Δx is a small increment in x, then the corresponding increment in y, Δy = f(x + Δx) – f(x), is approximately given as

Here, and Δx = 0.01kx

⇒ ΔS = (2πxtan(α)[tan(α) + sec(α)])(0.01kx)

∴ ΔS = 0.02kπx²tan(α)[tan(α) + sec(α)]

The percentage increase in S is,

⇒ Increase = 0.02k × 100%

∴ Increase = 2k%

Thus, the approximate increase in the total surface area of the cone is 2k%.

(ii) The volume of the cone is given by

From above, we have r = x tan(α).

On differentiating V with respect to x, we get

We know

Recall that if y = f(x) and Δx is a small increment in x, then the corresponding increment in y, Δy = f(x + Δx) – f(x), is approximately given as

Here, and Δx = 0.01kx

⇒ ΔV = (πx²tan²α)(0.01kx)

∴ ΔV = 0.01kπx³tan²α

The percentage increase in V is,

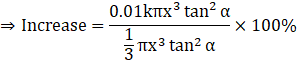
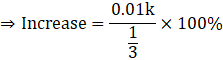
⇒ Increase = 0.03k × 100%

∴ Increase = 3k%

Thus, the approximate increase in the volume of the cone is 3k%.