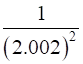
Let us assume that

Also, let x = 2 so that x + Δx = 2.002

⇒ 2 + Δx = 2.002

∴ Δx = 0.002

On differentiating f(x) with respect to x, we get

We know

When x = 2, we have

Recall that if y = f(x) and Δx is a small increment in x, then the corresponding increment in y, Δy = f(x + Δx) – f(x), is approximately given as

Here, and Δx = 0.002

⇒ Δf = (–0.25)(0.002)

∴ Δf = –0.0005

Now, we have f(2.002) = f(2) + Δf

⇒ f(2.002) = 0.25 – 0.0005

∴ f(2.002) = 0.2495

Thus,