Let us assume that

Also, let x = 32 so that x + Δx = 33

⇒ 32 + Δx = 33

∴ Δx = 1

On differentiating f(x) with respect to x, we get

We know

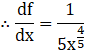
When x = 32, we have

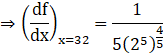
Recall that if y = f(x) and Δx is a small increment in x, then the corresponding increment in y, Δy = f(x + Δx) – f(x), is approximately given as

Here, and Δx = 1

⇒ Δf = (0.0125)(1)

∴ Δf = 0.0125

Now, we have f(33) = f(32) + Δf

⇒ f(33) = 2 + 0.0125

∴ f(33) = 2.0125

Thus, (33)^1/5 ≈ 2.0125