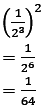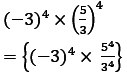Simplify and express the result in power notation with positive exponent.
(i) (-4)5 ÷ (-4)8
(ii)
(iii)
(iv) (3-7 ÷ 3-10) × 3-5
(v) 2-3 × (-7)-3
(i) Formula: am ÷ an = a(m-n)
By using above formula in question:
(-4)5 ÷ (-4)8
= (-4)5-8
= (-4)-3
= 1/(-4)3
= -1/64
(ii) Formula: (am)n = amn
By using above formula in question:
(iii) Formula:- am ÷ an = a(m-n)
= 54
= 625
(iv) Formula:- am ÷ an = a(m-n)
am × an = a{m+n}
By using above formula in question:
(3-7÷ 3-10) × 3-5
= (3 (-7+10)) × 3-5
= 33 × 3-5
= 3 (3-5)
= 3-2
= 1/9
(v) 2-3 × (-7)-3
= 1/23 – 1/73
= 1/8 × 1/343
= 1/2744
26