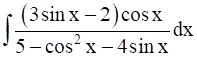
I = =

⇒ I =

Let, sin x = t ⇒ cos x dx = dt

∴ I =

As we can see that there is a term of t in numerator and derivative of t² is also 2t. So there is a chance that we can make substitution for t² – 4t + 4 and I can be reduced to a fundamental integration.

As,

∴ Let, 3t – 2 = A(2t – 4) + B

⇒ 3t – 2 = 2At – 4A + B

On comparing both sides –

We have,

2A = 3 ⇒ A = 3/2

–4A + B = –2 ⇒ B = 4A – 2 = 4

Hence,

I =

∴ I =

Let, I₁ = and I₂ =

Now, I = I₁ + I₂ ….eqn 1

We will solve I₁ and I₂ individually.

As, I₁ =

Let u = t² – 4t + 4 ⇒ du = (2t – 4)dx

∴ I₁ reduces to

Hence,

I₁ = {∵ }

On substituting value of u, we have:

I₁ =

I₁ = ….eqn 2

∵ I₂ =

⇒ I₂ =

Using: a² – 2ab + b² = (a – b)²

We have:

I₂ =

As,

∴ I₂ = + C …eqn 3

From eqn 1, we have:

I = I₁ + I₂

Using eqn 2 and 3, we get –

I =

Putting value of t in I:

I = …..ans