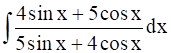
Ideas required to solve the problems:

* Integration by substitution: A change in the variable of integration often reduces an integral to one of the fundamental integration. If derivative of a function is present in an integration or if chances of its presence after few modification is possible then we apply integration by substitution method.

* Knowledge of integration of fundamental functions like sin, cos ,polynomial, log etc and formula for some special functions.

Let, I =

To solve such integrals involving trigonometric terms in numerator and denominators. We use the basic substitution method and to apply this simply we follow the undermentioned procedure-

If I has the form

Then substitute numerator as -

Where A, B and C are constants

We have, I =

As I matches with the form described above, So we will take the steps as described.

∴

⇒ {

⇒

Comparing both sides we have:

C = 0

5B - 4A = 4

4B + 5A = 5

On solving for A ,B and C we have:

A =9/41, B = 40/41 and C = 0

Thus I can be expressed as:

I =

I =

∴ Let I₁ = and I₂ =

⇒ I = I₁ + I₂ ….equation 1

I₁ =

Let, 4 cos x + 5sin x = u

⇒ (-4sin x + 5cos x)dx = du

So, I₁ reduces to:

I₁ =

∴ I₁ = …..equation 2

As, I₂ =

⇒ I₂ = …..equation 3

From equation 1, 2 and 3 we have:

I =

∴ I =