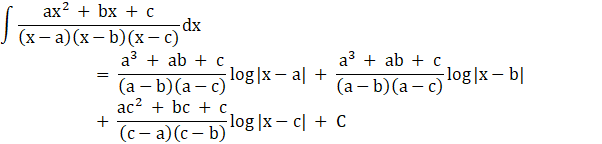Evaluate the following integral:
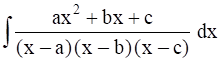 , where a, b, c are distinct.
, where a, b, c are distinct.
Denominator is factorised, so let separate the fraction through partial fraction, hence let
![]()
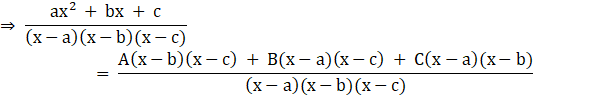
⇒ ax2 + bx + c = A(x – b)(x – c) + B(x – a)(x – c) + C(x – a)(x – b)……(ii)
We need to solve for A, B and C. One way to do this is to pick values for x which will cancel each variable.
Put x = a in the above equation, we get
⇒ a(a)2 + b(a) + c = A(a – b)(a – c) + B(a – a)(a – c) + C(a – a)(a – b)
⇒ a3 + ab + c = (a – b)(a – c)A + 0 + 0
![]()
Now put x = b in equation (ii), we get
⇒ a(b)2 + b(b) + c = A(b – b)(b – c) + B(b – a)(b – c) + C(b – a)(b – b)
⇒ ab2 + b2 + c = 0 + (b – a)(b – c)B + 0
![]()
Now put x = c in equation (ii), we get
![]()
![]()
![]()
We put the values of A, B, and C values back into our partial fractions in equation (i) and replace this as the integrand. We get
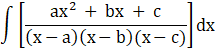
![]()
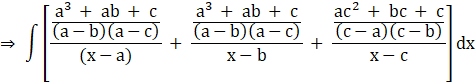
Split up the integral,
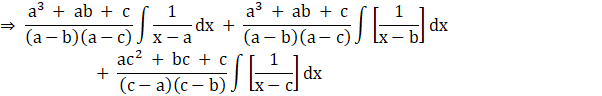
Let substitute
u = x – a ⇒ du = dx,
y = x – b ⇒ dy = dx and
z = x – c ⇒ dz = dx, so the above equation becomes,
![]()
On integrating we get
![]()
Substituting back, we get
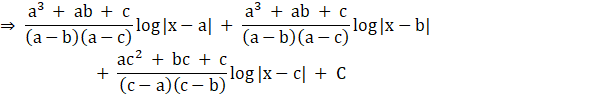
Note: the absolute value signs account for the domain of the natural log function (x>0).
Hence,