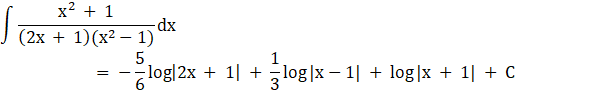Evaluate the following integral:
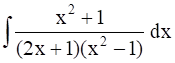
Denominator is factorized, so let separate the fraction through partial fraction, hence let
![]()
![]()
![]()
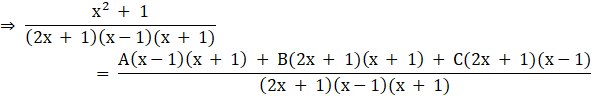
⇒ x2 + 1 = A(x – 1)(x + 1) + B(2x + 1)(x + 1) + C(2x + 1)(x – 1)……(ii)
We need to solve for A, B and C. One way to do this is to pick values for x which will cancel each variable.
Put x = 1 in the above equation, we get
⇒ 12 + 1 = A(1 – 1)(1 + 1) + B(2(1) + 1)(1 + 1) + C(2(1) + 1)(1 – 1)
⇒ 2 = 0 + 6B + 0
![]()
Now put ![]() in equation (ii), we get
in equation (ii), we get
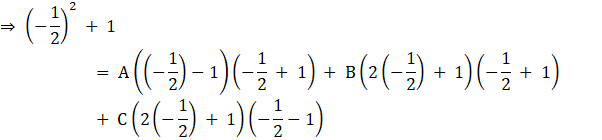
![]()
![]()
Now put x = – 1 in equation (ii), we get
⇒ ( – 1)2 + 1 = A( – 1 – 1)( – 1 + 1) + B(2( – 1) + 1)( – 1 + 1) + C(2( – 1) + 1)( – 1 – 1)
⇒ 2 = 0 + 0 + 2C
⇒ C = 1
We put the values of A, B, and C values back into our partial fractions in equation (i) and replace this as the integrand. We get
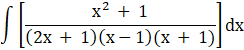
![]()
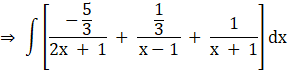
Split up the integral,
![]()
Let substitute
u = x – 1⇒ du = dx,
y = x + 1 ⇒ dy = dx and
z = 2x + 1 ⇒ dz = 2dx so the above equation becomes,
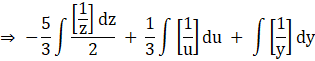
On integrating we get
![]()
Substituting back, we get
![]()
Note: the absolute value signs account for the domain of the natural log function (x>0).
Hence,