Evaluate the following integral:
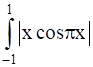 dx
dx
Let f(x) = ![]()
Substituting x = – x in f(x)
f( – x) = ![]()
f(x) = f( – x)
![]() it is an even function
it is an even function
![]() ………(1)
………(1)
Now,
f(x) = |x cosπx| = x cosπx; for x![]() [0,12]
[0,12]
= – x cosπx; for x![]() [1/2,1]
[1/2,1]
Using interval addition property of integration, we know that
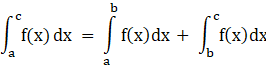
Equation 1 can be written as
2[![]() ]
]
Putting the limits in above equation
= 2{[(x/π)sin![]() x + (1/π2)cosπx]01/2 – [(x/π
x + (1/π2)cosπx]01/2 – [(x/π![]() sin
sin![]() x + (1/π2)cosπx]11/2}
x + (1/π2)cosπx]11/2}
= 2{[(1/2π) – (1/π2)] – [( – 1/π2) – (1/2π)]}
= 2/π
35