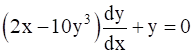
Given

This is a first order linear differential equation of the form

Here, and Q = 10y²

The integrating factor (I.F) of this differential equation is,

We have

[∵ m log a = log a^m]

∴ I.F = y² [∵ e^{log x} = x]

Hence, the solution of the differential equation is,

Recall

⇒ xy² = 2y⁵ + c

∴ x = 2y³ + cy^–2

Thus, the solution of the given differential equation is x = 2y³ + cy^–2