Solve each of the following linear programming problems by graphical method.
Show the solution zone of the following inequalities on a graph paper:
5x + y ≥ 10
x + y ≥ 6
x + 4y ≥ 12
x ≥ 0, y ≥ 0
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
Given,
Z = 3x + 2y
Constraints:
5x + y ≥ 10
x + y ≥ 6
x + 4y ≥ 12
x ≥ 0, y ≥ 0
First convert the given inequations into corresponding equations and plot them:
5x + y ≥ 10 → 5x + y = 10(corresponding equation)
Two coordinates required to plot the equation are obtained as:
Put, x = 0 ⇒ y = 10 (0,10) - - - - first coordinate.
Put, y = 0 ⇒ x = 2 (2,0) - - - - second coordinate
Join them to get the line.
As we know, Linear inequation will be a region in the plane, and we observe that the equation divides the XY plane into 2 halves only, so we need to check which region represents the given inequation,
If the given line does not pass through origin then just put (0,0) to check whether inequation is satisfied or not. If it satisfies the inequation origin side is the required region else the other side is the solution.
Similarly, we repeat the steps for other inequation also and find the common region.
x + y ≥ 6 → x + y = 6 (corresponding equation)
Two coordinates required to plot the equation are obtained as:
Put, x = 0 ⇒ y = 6 (0,6) - - - - first coordinate.
Put, y = 0 ⇒ x = 6 (6,0) - - - - second coordinate
x + 4y ≥ 12 → x + 4y = 12 (corresponding equation)
Two coordinates required to plot the equation are obtained as:
Put, x = 0 ⇒ y = 3 (0,3) - - - - first coordinate.
Put, y = 0 ⇒ x = 12 (12,0) - - - - second coordinate
x = 0 is the y - axis and y = 0 is the x - axis.
Hence, we have the following plot:
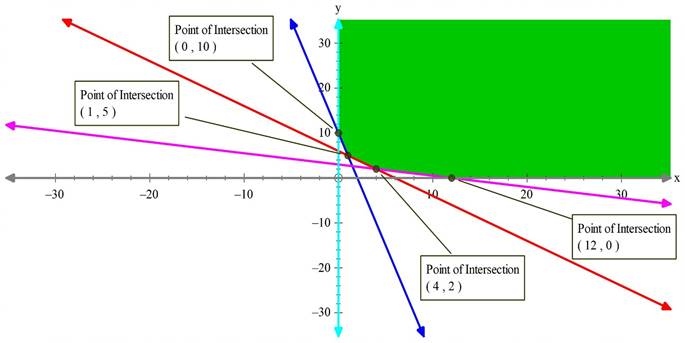
The shaded region in the above figure represents the region of a feasible solution.
Now to minimize our objective function, we need to find the coordinates of the corner points of the shaded region.
We can determine the coordinates graphically our by solving equations. But choose only those equations to solve which gives one of the corner coordinates of the feasible region.
Solving x + 4y = 12 and x + y = 6 gives (4,2)
Similarly solve other combinations by observing graph to get other coordinates.
From the figure we have obtained coordinates of corners as:
(4,2),(12,0),(1,5) and (0,10)
Now we have coordinates of the corner points so we will put them one by one to our objective function and will find at which point it is maximum.
∵ Z = 3x + 2y
∴ Z at (4,2) = 4×3 + 2×2 = 16
Z at (12,0) = 3×12 + 2×0 = 36
Z at (1,5) = 3× 1 + 2× 5 = 13
Z at (0,10) = 3× 0 + 2×10 = 20
As the region is unbounded as we can’t say blindly that Z = 13 is minimum because there might be other points in feasible region that may Make Z even lesser.
So we need to check whether Z is minimum or not or Z lesser than 13 or not.
For this we define inequation using the optimal function if the solution region of the inequation does not coincide with the feasible region, it means it has a maxima
Inequation: 3x + 2y < 13
It will be towards origin side, so it will not overlap with the feasible region.
∴ Minima are possible.
Minimum is possible and minimum occurs at x = 1 and y = 5 and value is Z = 13.