A man wins a rupee for head and loses a rupee for tail when the coin is tossed. Suppose that he tosses once and quits if he wins but tries once more if he loses on the first toss. Find the probability distribution of the number of rupees the man wins.

Question

Philoid · Accepted Answer

Let X be the number of rupees the man won/lost.

Let n be the number of throws required to get a head.

We have two cases, that is

(i). The man tosses once, head comes up, and he quits. (head means he won)

(ii). The man tosses once; tail comes up then he tosses again, tail comes up. (tail means he lost)

(ii). The man tosses, tail comes up then he tosses again, head comes up. (tail means he lost & head means he won)

In Case (i),

The man tosses once, head comes up, and he quits.

Here, number of throws (n) = 1

Amount won/lost (X) = 1

In Case (ii),

The man tosses once; tail comes up then he tosses again, tail comes up.

Here, number of throws (n) = 2

Amount won/lost (X) = -2

In Case (iii),

The man tosses once, tail comes up then he tosses again, head comes up.

Here, number of throws (n) = 2

Amount won/lost (X) = 0

We have the table:

Thus, the probability distribution is

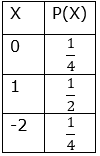
Hence, the answer is obtained.