Book: RD Sharma - Mathematics (Volume 2)
Chapter: 33. Binomial Distribution
Subject: Maths - Class 12th
Q. No. 29 of Exercise 33.1
Listen NCERT Audio Books - Kitabein Ab Bolengi
A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart, (ii) the probability of drawing a heart is greater than 3/4?
We know that there are 52 cards in a pack of cards.
And there are 13 cards of each suit.
Let p be the probability of drawing a card of heart from a pack of 52 cards.
Then,
[∵ there are 13 cards of heart in the pack]
Also, p + q = 1
Where if p is the probability of getting a heart out of 52 cards, then q is the probability of not getting a heart out of 52 cards.
⇒ q = 1 – p
Putting the value of p in the above equation, we get
Now, let the card be drawn n times.
And let X denote the number of hearts drawn out of a pack of 52 cards.
Then, the binomial distribution is given by,
P (X = r) = nCrprqn-r
Putting 
and 
above, we get
…(A)
Where r = 0, 1, 2, 3… n
(i). We need to find the number of times a card can be drawn so that at least there is an even chance of drawing a heart.
In simple words, since n is the number of times a card is drawn, we need to find the smallest n for which P (X = 0) is less than 1/4 satisfies. 
So,
From equation A, we have
First, put n = 0.
But 1 ≮ 0.25
Now, put n = 1.
⇒ 0.75 < 0.25
But 0.75 ≮ 0.25
Now, put n = 2.
⇒ 0.5625 < 0.25
But 0.5626 ≮ 0.25
Now, put n = 3.
⇒ 0.42 < 0.25
But 0.42 ≮ 0.25
Now, put n = 4.
⇒ 0.31 < 0.25
But 0.31 ≮ 0.25
Now, put n = 5.
⇒ 0.23 < 0.25
Thus, smallest n = 5.
∴, we must draw cards at least 5 times.
(ii). We need to find the number of times a card must be drawn so that the probability of drawing a heart is more than 3/4.
If P (X = 0) is the probability of not drawing a heart at all.
Then, 1 – P (X = 0) is the probability of drawing a heart out of 52 cards.
According to the question,
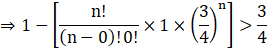
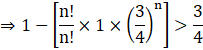
First, put n = 0.
But 1 ≮ 0.25
Now, put n = 1.
⇒ 0.75 < 0.25
But 0.75 ≮ 0.25
Now, put n = 2.
⇒ 0.5625 < 0.25
But 0.5626 ≮ 0.25
Now, put n = 3.
⇒ 0.42 < 0.25
But 0.42 ≮ 0.25
Now, put n = 4.
⇒ 0.31 < 0.25
But 0.31 ≮ 0.25
Now, put n = 5.
⇒ 0.23 < 0.25
Thus, smallest n = 5.
∴, we must draw cards at least 5 times.
