Given that, a certain kind of component will survive a given shock

Let p be the probability that component survives the shock test.

Then,

If p is the probability that component survives the shock test, then q is the probability that the component doesn’t survive the shock test.

⇒ p + q = 1

⇒ q = 1 – p

Let X denote a random variable that represents the components that survive the shock test out of the 5 components tested.

The probability that r components out of n components survive the shock test is given by the binomial distribution.

P (X = r) = ⁿC_rp^rq^n-r

Here, n = 5 (sample components tested)

And

We can re-write it as,

…(A)

(i). We need to find the probability that among 5 components tested exactly 2 will survive.

Then, put r = 2 in equation (A). We have

⇒ P (X = 2) = 0.0879

∴, the probability that exactly 2 components out of 5 will survive the test is 0.0879.

(ii). We need to find the probability that among the 5 components tested at most 3 will survive.

So, this can be give in two ways:

(a). Probability that out of 5 components at most 3 will survive = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)

(b). Probability that out of 5 components at most 3 will survive = 1 – [P (X = 4) + P (X = 5)]

Let us solve it by using the formula in (b).

So, let us find out P (X = 4).

Putting r = 4 in equation (A), we get

Now, let us find out P (X = 5).

Putting r = 5 in equation (A), we get

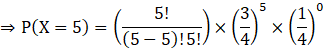
Using the values of P (X = 4) & P (X = 5) in formula (b), we get

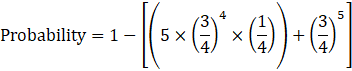
⇒ Probability = 0.3672

∴, the probability that out of 5 components at most 3 will survive is 0.3672.