We have been given that, the probability that a bomb dropped from an airplane will strike a certain target is 0.2.

Also, that 6 bombs are dropped.

Let p be the probability that a bomb dropped from an airplane will strike a certain target.

Then, q is the probability that a bomb dropped from an airplane will not strike a certain target.

⇒ p = 0.2

We know that, p + q = 1

⇒ q = 1 – p

Let X be a random variable the represents the number of bombs that strike the target.

Then, the probability that r bombs strike the target out of n bombs is given by,

P (X = r) = ⁿC_rp^rq^n-r

Where n = 6

Let us put the values of n, p, and q in the above equation.

…(A)

(i). We need to find the probability that exactly 2 will strike the target out of 6 bombs.

Probability is given by,

Probability = P (X = 2)

So, put r = 2 in equation (A).

⇒ Probability = 0.24576

∴, the probability that exactly 2 will strike the target out of 6 bombs is 0.24576.

(ii). We need to find the probability that at least 2 will strike the target out of 6 bombs.

Probability is given by,

Probability = P (X ≥ 2)

This can also be written as,

Probability = 1 – P (X < 2)

⇒ Probability = 1 – [P (X = 0) + P (X = 1)]

Let us find the value of P (X = 0).

For this, put r = 0 in equation (A).

Now, let us find the value of P (X = 1).

For this, put r = 0 in equation (A).

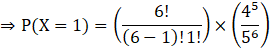
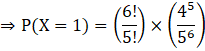
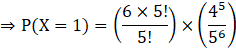
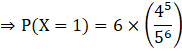
Now, putting all these values in 1 – [P (X = 0) + P (X = 1)].

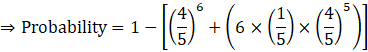
⇒ Probability = 0.345

∴, the probability that at least 2 will strike the target out of 6 bombs is 0.345.