Book: RD Sharma - Mathematics (Volume 2)
Chapter: 33. Binomial Distribution
Subject: Maths - Class 12th
Q. No. 40 of Exercise 33.1
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Ten eggs are drawn successively, with replacement, from a lot containing 10% defective eggs. Find the probability that there is a least one defective egg.
Given that, 10 eggs are drawn successively.
Defective eggs in the lot = 10%
Let p be the probability that the eggs drawn from the lot are defective.
⇒ p = 10%
Then, q is the probability that the eggs drawn from the lot is not defective.
And, p + q = 1
⇒ q = 1 – p
Let X be a random variable that represents defective eggs picked out of n eggs from the lot.
Then, the probability of taking r defective eggs out of n eggs from the lot is given by,
P (X = r) = nCrprqn-r
Here, n = 10
Putting the values of n, p, and q in the above formula, we get
…(i)
We need to find the probability of getting at least one defective egg from the lot.
This is represented as,
Probability = P (X ≥ 1)
This is also written as,
P (X ≥ 1) = P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4) + P (X = 5) + P (X = 6) + P (X = 7) + P (X = 8) + P (X = 9) + P (X = 10)
Or
P (X ≥ 1) = 1 – P (X < 1)
⇒ P (X ≥ 1) = 1 – P (X = 0)
Putting r = 0 in P (X = r) formula in (i), we get
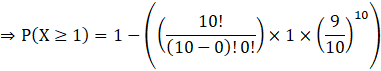
∴, the probability of getting at least one defective egg from the lot is 
.
