Book: RD Sharma - Mathematics (Volume 2)
Chapter: 33. Binomial Distribution
Subject: Maths - Class 12th
Q. No. 41 of Exercise 33.1
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
In a 20-question true-false examination suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answer ‘true’; if it falls tails, he answers ‘false’. Find the probability that he answers at least 12 questions correctly.
Given that, there are 20 questions of true-false exam.
If the coin falls head, he answers “true.”
If the coin falls tail, he answers “false.”
Let p be the probability of a correct answer.
That is, p = getting a head and a right answer to be “true” for a question or getting a tail and a right answer to be “false” for a question.
Then, q is the probability of the answer to be incorrect.
And, p + q = 1
⇒ q = 1 – p
Let X denote a random variable representing the number of correct answers out of 20 questions.
Then, the probability of getting r correct answers out of n answered questions is given by,
P (X = r) = nCrprqn-r
Here, n = 20 [∵ there are 20 questions in total]
Putting values of n, p, and q in the above equation, we get
…(i)
We need to find the probability that he answers at least 12 questions correctly.
This can be represented as,
Probability = P (X ≥ 12)
It can be written as,
P (X ≥ 12) = P (X = 12) + P (X = 13) + P (X = 14) + P (X = 15) + P (X = 16) + P (X = 17) + P (X = 18) + P (X = 19) + P (X = 20) …(ii)
Put r = 12, 13, 14, 15, 16, 17, 18, 19, 20 in equation (i) subsequently and substitute in (ii), we get
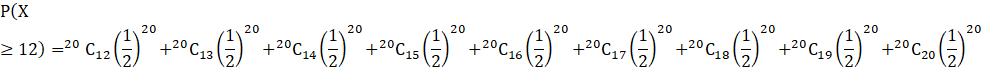
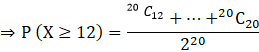
∴, we have got the required probability.
