RD Sharma - Mathematics (Volume 2)

Book: RD Sharma - Mathematics (Volume 2)

Chapter: 33. Binomial Distribution

Subject: Maths - Class 12th

Q. No. 44 of Exercise 33.1

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

44

A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100. What is the probability that he will win a prize

i. at least once


ii. exactly once


iii. at least twice?

Given that, a person buys a lottery ticket in 50 lotteries.


The probability of winning a prize is 1/100.


Let p be the probability of winning a prize.


Then,


And q be the probability of not winning a prize.


We can write,


p + q = 1


⇒ q = 1 – p





Let X be a random variable representing the number of times the person wins the lottery out of n lotteries.


Then, the probability of the person winning the lottery r times out of n times is given by this Binomial distribution.


P (X = r) = nCrprqn-r


Here, n = 50


So, putting the value of n, p, and q in the formula of P (X = r), we get


…(A)


(i). We need to find the probability that he will win the prize at least once.


The probability is given by,


Probability = P (X ≥ 1)


Or this can be written as,


P (X ≥ 1) = 1 – P (X < 1)


⇒ P (X ≥ 1) = 1 – P (X = 0) …(B)


So, put r = 0 in equation (A) and then substitute in equation (B), we get






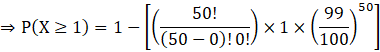
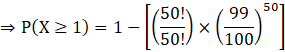
Thus, the probability that he will win the prize at least once is .


(ii). We need to find the probability that he will win the prize exactly once.


The probability is given by,


Probability = P (X = 1)


Put r = 1 in equation (A), we get







Thus, the probability that he will win the prize exactly once is .


(iii). We need to find the probability that he will win at least twice.


The probability is given by,


Probability = P (X ≥ 2)


Or can be expressed as,


P (X ≥ 2) = 1 – P (X < 2)


⇒ P (X ≥ 2) = 1 – [P (X = 0) + P (X = 1)] …(B)


Put r = 0 and r = 1 in equation (A) one by one and then substitute it in the equation (B), we get









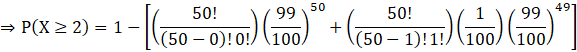
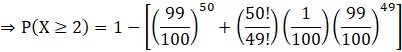
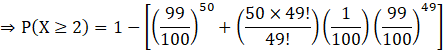
Thus, the probability that he will win the prize at least twice is .


Chapter Exercises

Exercise 33.2
Exercise 33.1
Very Short Answer
MCQ

More Exercise Questions

26

A man wins a rupee for head and loses a rupee for tail when the coin is tossed. Suppose that he tosses once and quits if he wins but tries once more if he loses on the first toss. Find the probability distribution of the number of rupees the man wins.
27

Five dice are thrown simultaneously. If the occurrence of 3, 4 or 5 in a single die is considered a success, find the probability of at least 3 successes.
28

The items produced by a company contain 10% defective items. Show that the probability of getting 2 defective items in a sample of 8 items is .
29

A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart, (ii) the probability of drawing a heart is greater than 3/4?
30

The mathematics department has 8 graduate assistants who are assigned to the same office. Each assistant is just likely to study at home as in the office. How many desks must there be in the office so that each assistant has a desk at least 90% of the time?
31

An unbiased coin is tossed 8 times. Find, by using binomial distribution, the probability of getting at least 6 heads.
32

Six coins are tossed simultaneously. Find the probability of getting

i. 3 heads


ii. no heads


iii. at least one head
33

Suppose that a radio tube inserted into a certain type of set has probability 0.2 of functioning more than 500 hours. If we test 4 tubes at random what is the probability that exactly three of these tubes function for more than 500 hours?
34

The probability that a certain kind of component will survive a given shock test is 3/4. Find the probability that among the 5 components tested

i. exactly 2 will survive


ii. at most 3 will survive
35

Assume that the probability that a bomb dropped from an airplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that

i. exactly 2 will strike the target.


ii. at least 2 will strike the target.
36

It is known that 60% of mice inoculated with serum are protected from a certain disease. If 5 mice are inoculated, find the probability that

i. none contract the disease


ii. more than 3 contract the disease.
37

An experiment succeeds twice as often as it fails. Find the probability that in the next 6 trials there will be at least 4 successes.
38

In a hospital, there are 20 kidney dialysis machines and that the chance of any one of them to be out of service during a day is 0.02. Determine the probability that exactly 3 machines will be out of service on the same day.
39

The probability that a student entering a university will graduate is 0.4. Find the probability that out of 3 students of the university:

i. none will graduate,


ii. The only one will graduate,


iii. All will graduate.
40

Ten eggs are drawn successively, with replacement, from a lot containing 10% defective eggs. Find the probability that there is a least one defective egg.
41

In a 20-question true-false examination suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answer ‘true’; if it falls tails, he answers ‘false’. Find the probability that he answers at least 12 questions correctly.
42

Suppose X has a binomial distribution with n=6 and p=1/2. Show that X = 3 is the most likely outcome.
43

In a multiple choice examination with three possible answers for each of the five questions out of which only one is correct, what is the probability that a candidate would get four or more correct answers just by guessing?
44

A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100. What is the probability that he will win a prize

i. at least once


ii. exactly once


iii. at least twice?
45

The probability of a shooter hitting a target is 3/4. How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
46

How many times must a man toss a fair coin so that the probability of having at least one head is more than 90%?
47

How many times must a man toss a fair coin so that the probability of having at least one head is more than 80%?
48

A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability distribution of the number of successes.
49

From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
50

Find the probability that in 10 throws of a fair die a score which is a multiple of 3 will be obtained in at least 8 of the throws.
51

A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.
52

The probability of a man hitting a target is 0.25. He shoots 7 times. What is he probability of his hitting at least twice?
53

A factory produces bulbs. The probability that one bulb is defective is 1/50, and they are packed in boxes of 10. From a single box, find the probability that

i. none of the bulbs is defective


ii. exactly two bulbs are defective


iii. more than 8 bulbs work properly.
54

A box has 20pens of which 2 are defective. Calculate the probability that out of 5 pens drawn one by one with replacement, at most 2 are defective.

Students Store