Let the man toss the coin n times.

Let p be the probability of getting a head in a toss.

Then, q is the probability of getting a tail in a toss.

Since the coin has only two outcomes, so the probability of getting a head = 1/2

Also, p + q = 1

⇒ q = 1 – p

Let X be a random variable that represents a number of occurrence of the head in n tosses of a fair coin.

Then, the probability of getting r number of heads out of total n tosses is given by this Binomial distribution.

P (X = r) = ⁿC_rp^rq^n-r

Substituting the value of p and q in the above equation, we get

…(i)

We need to find the number of times the man must toss a fair coin so that the probability of having at least one head is more than 90%.

We can represent it as,

P (getting atleast one head) > 90%

⇒ P (X ≥ 1) > 90%

⇒ 1 – P (X < 1) > 90% [∵ P (X ≥ 1) = 1 – P (X < 1)]

⇒ 1 – P (X = 0) > 90% [∵ P (X < 1) = P (X = 0)]

Put r = 0 in equation (i) and then, substituting it in the above equation.

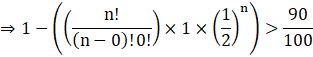
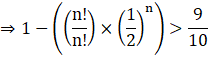
⇒ 2ⁿ > 10

Now, we need to find the minimum value of n that satisfy this inequality.

Put n = 0.

⇒ 2⁰ > 10

⇒ 1 > 10

But 1 ≯ 10.

Put n = 1.

⇒ 2¹ > 10

⇒ 2 > 10

But 2 ≯ 10.

Put n = 2.

⇒ 2² > 10

⇒ 4 > 10

But 4 ≯ 10.

Put n = 3.

⇒ 2³ > 10

⇒ 8 > 10

But 8 ≯ 10.

Put n = 4.

⇒ 2⁴ > 10

⇒ 16 > 10

It is true.

Thus, the minimum n that satisfy this inequality is 4.

Hence, the man should toss the coin 4 or more times.