Given that, a die is thrown 5 times.

Let p be the probability of getting an odd number in a throw.

Since there are 6 possible outcomes in a throw of a die. That is, {1, 2, 3, 4, 5, 6}

And there are 3 odd numbers out of these 6 outcomes. That is, {1, 3, 5}

Then, let q be the probability of getting an even number in a throw.

And we know that, p + q = 1

⇒ q = 1 – p

Let X be a random variable representing a number of odd numbers in n throw of a die.

Then, the probability of getting r odd numbers out of n throw of the die can be given as,

P (X = r) = ⁿC_rp^rq^n-r

Here, n = 5

Putting values of n, p, and q in the above formula. We get

…(i)

We need to find the probability that an odd number will come up exactly three times.

It is given by,

Probability = P (X = 3)

Put r = 3 in equation (i) to find P (X = 3), we get

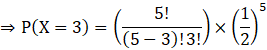
Thus, the probability of getting an odd number to come up exactly three times is 5/16.