Book: RD Sharma - Mathematics (Volume 2)
Chapter: 33. Binomial Distribution
Subject: Maths - Class 12th
Q. No. 52 of Exercise 33.1
Listen NCERT Audio Books - Kitabein Ab Bolengi
The probability of a man hitting a target is 0.25. He shoots 7 times. What is he probability of his hitting at least twice?
Given that, the probability of a man hitting a target is 0.25.
And he shoots 7 times in total.
Let p be the probability of hitting the target.
Then,
p = 0.25
Then, q be the probability of not hitting the target.
And we know that,
p + q = 1
⇒ q = 1 – p
Let X be a random variable representing the number of times the man hits the target out of n shoots.
Then, the probability of hitting the target r times out of n times is given by,
P (X = r) = nCrprqn-r
Here, n = 7
Putting the values of n, p, and q in the above equation, we get
…(i)
We need to find the probability of hitting the target at least twice.
This can be expressed as,
Probability = P (X ≥ 2)
Or
P (X ≥ 2) = 1 – P (X < 2)
⇒ P (X ≥ 2) = 1 – [P (X = 0) + P (X = 1)]
So, put r = 0, 1 in equation (i) to get P (X = 0) and P (X = 1) respectively and then, substitute in the above formula.
We get
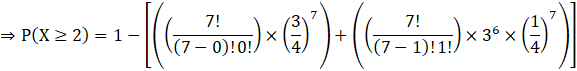
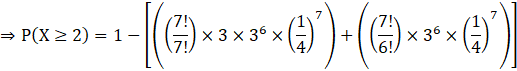
Thus, the probability of hitting the target at least twice is 4547/8192.
