Given that, a box has 20 pens out of which 2 are defective.

Let p be the probability of a number of pens being defective out of 20 pens.

Then, q be the probability of a number of pens not being defective.

Also, p + q = 1

⇒ q = 1 – p

Let X be a random variable representing a number of defective pens out of 5 pens.

Then, the probability of getting r defective pens out of n pens is given by,

P (X = r) = ⁿC_rp^rq^n-r

Here, n = 5

Putting all the values of n, p, and q in the above equation, we get

…(i)

We need to find the probability that at most 2 pens are defective out of 5 pens.

This can be represented as,

Probability = P (X ≤ 2)

Or

P (X ≤ 2) = P (X = 0) + P (X = 1) + P (X = 2)

Put r = 0, 1, 2 in equation (i) to find P (X = 0), P (X = 1) and P (X = 2), and then substitute in the above equation. We get,

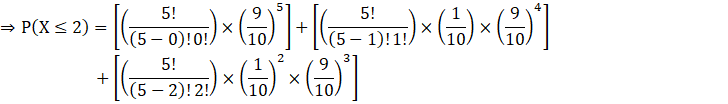
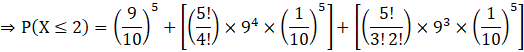
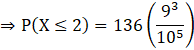
Thus, the probability that at most 2 pens are defective out of 5 pens is .