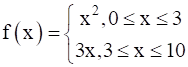The relation g is defined by 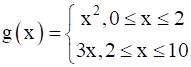
Show that f is a function and g is not a function.
Given ![]() and
and ![]()
Let us first show that f is a function.
When 0 ≤ x ≤ 3, f(x) = x2.
The function x2 associates all the numbers 0 ≤ x ≤ 3 to unique numbers in R.
Hence, the images of {x ∈ Z: 0 ≤ x ≤ 3} exist and are unique.
When 3 ≤ x ≤ 10, f(x) = 3x.
The function x2 associates all the numbers 3 ≤ x ≤ 10 to unique numbers in R.
Hence, the images of {x ∈ Z: 3 ≤ x ≤ 10} exist and are unique.
When x = 3, using the first definition, we have
f(3) = 32 = 9
When x = 3, using the second definition, we have
f(3) = 3(3) = 9
Hence, the image of x = 3 is also distinct.
Thus, as every element of the domain has an image and no element has more than one image, f is a function.
Now, let us show that g is not a function.
When 0 ≤ x ≤ 2, g(x) = x2.
The function x2 associates all the numbers 0 ≤ x ≤ 2 to unique numbers in R.
Hence, the images of {x ∈ Z: 0 ≤ x ≤ 2} exist and are unique.
When 2 ≤ x ≤ 10, g(x) = 3x.
The function x2 associates all the numbers 2 ≤ x ≤ 10 to unique numbers in R.
Hence, the images of {x ∈ Z: 2 ≤ x ≤ 10} exist and are unique.
When x = 2, using the first definition, we have
g(2) = 22 = 4
When x = 2, using the second definition, we have
g(2) = 3(2) = 6
Here, the element 2 of the domain is associated with two elements distinct elements 4 and 6.
Thus, g is not a function.