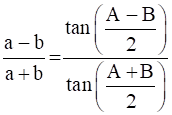
Let a, b, c be the sides of any triangle ABC. Then by applying the sine rule, we get

⇒a = k sin A

Similarly, b = k sin B

So, a - b = k(sin A - sin B)

And a + b = k(sin A + sin B)

So, the given LHS becomes,

But,

Substituting the above values in equation (i), we get

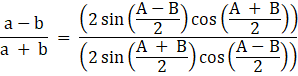
Rearranging the above equation we get,

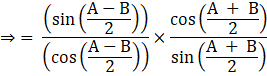
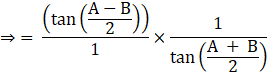
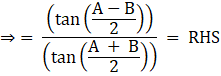
Hence proved