Let a, b, c be the sides of any triangle ABC. Then by applying the sine rule, we get

⇒ a = k sin A, b = k sin B, c = k sin C

So the LHS of the given equation, we get

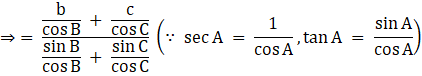
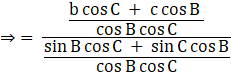
Substituting values from sine law, we get

Now consider the second part of the equation, we get

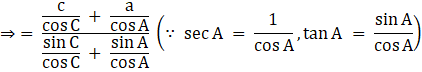
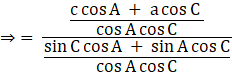
Substituting values from sine law, we get

Now consider the third part of the equation, we get

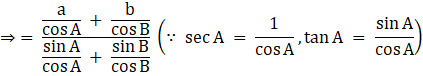
Substituting values from sine law, we get

From equation (i), (ii), and (iii), we get

Hence proved