Show that the point (x, y) given by 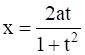 and
and 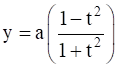 lies on a circle for all real values of t such that - 1 ≤ t ≤ 1, where a is any given real number.
lies on a circle for all real values of t such that - 1 ≤ t ≤ 1, where a is any given real number.
Given:
⇒ ![]()
⇒ ![]()
We need to prove that the point (x, y) lies on a circle for real values of t such that - 1≤t≤1, where a is any given real number.
Consider x2 + y2,
⇒ 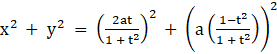
⇒ 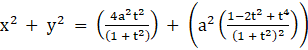
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ x2 + y2 = a2
The point (x,y) lies on a circle.
∴Thus proved.
18