ABCD is a square whose side is a; taking AB and AD as axes, prove that the equation of the circle circumscribing the square is x 2 + y 2 – a(x + y) = 0.

Question

Philoid · Accepted Answer

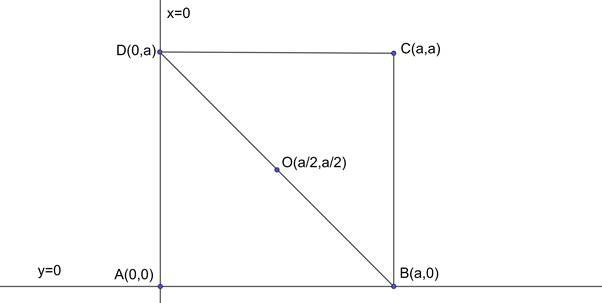
Given that we need to find the equation of the circle which circumscribes the square ABCD of side a.

It is also told that AB and AD are assumed as x and y - axes.

Assuming A as origin, We get the points B(a,0) and D(0,a).

So, we need to find the circle which is passing through the points A(0,0), B(a,0) and D(0,a).

We know that the standard form of the equation of the circle is given by:

⇒ x² + y² + 2fx + 2gy + c = 0 ..... (1)

Substituting A(0,0) in (1), we get,

⇒ 0² + 0² + 2f(0) + 2g(0) + c = 0

⇒ c = 0 ..... (2)

Substituting B(a,0) in (1), we get,

⇒ a² + 0² + 2f(a) + 2g(0) + c = 0

⇒ a² + 2fa + c = 0 ..... (3)

Substituting D(0,a) in (1), we get,

⇒ 0² + a² + 2f(0) + 2g(a) + c = 0

⇒ a² + 2ga + c = 0 ..... (4)

On solving (2), (3) and (4) we get,

⇒

Substituting these values in (1), we get

⇒

⇒ x² + y² - ax - ay = 0

⇒ x² + y² - a(x + y) = 0

∴Thus proved.

ABCD is a square whose side is a; taking AB and AD as axes, prove that the equation of the circle circumscribing the square is x2 + y2 – a(x + y) = 0.

ABCD is a square whose side is a; taking AB and AD as axes, prove that the equation of the circle circumscribing the square is x² + y² – a(x + y) = 0.