Find the equations of the circles which pass through the origin and cut off equal chords of √2 units from the lines y = x and y = - x.
We need to find the equations of the circles which pass through the origin and having chords of ![]() units from the lines y = x and y = - x.
units from the lines y = x and y = - x.
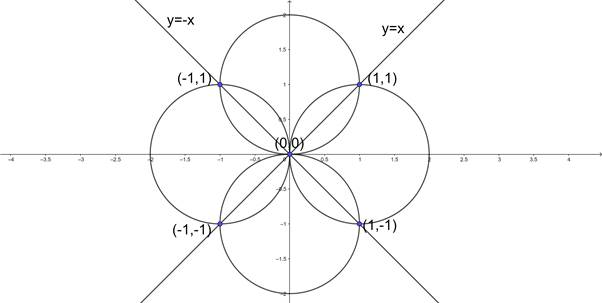
From the figure, we can see that the chords of length √2 units from origin O exists at points A(1,1), B(1, - 1), C(- 1,1) and D(- 1, - 1).
Let us find the distances AB, AC, BD, CD.
We know that distance between two points (x1,y1) and (x2,y2) is ![]() .
.
⇒ ![]()
⇒ ![]()
⇒ AB = 2
Similarly AD = BC = CD = 2 units.
We have got right-angled triangles OAB, OAD, OBC, OCD.
We need to find the circle that circumscribes these circles.
We know that the circumcentre of a right-angled triangle is the mid - point of the hypotenuse.
⇒ Circumcentre (C1) of OAB = ![]()
⇒ C1 = (1,0)
The radius of the circle is half of the length of the hypotenuse.
⇒ ![]()
⇒ r1 = 1 units.
We know that the equation of the circle with centre (p, q) and having radius ‘r’ is given by:
⇒ (x - p)2 + (y - q)2 = r2
Now we substitute the corresponding values in the equation to get the circle’s equation for ΔOAB:
⇒ ![]()
⇒ x2 - 2x + 1 + y2 = 1
⇒ x2 + y2 - 2x = 0
⇒ Circumcentre (C2) of OAD = ![]()
⇒ C2 = (0,1)
The radius of the circle is half of the length of the hypotenuse.
⇒ ![]()
⇒ r2 = 1 units.
We know that the equation of the circle with centre (p, q) and having radius ‘r’ is given by:
⇒ (x - p)2 + (y - q)2 = r2
Now we substitute the corresponding values in the equation to get the circle’s equation for ΔOAD:
⇒ ![]()
⇒ x2 + y2 - 2y + 1 = 1
⇒ x2 + y2 - 2y = 0
⇒ Circumcentre (C3) of OBC = ![]()
⇒ C3 = (0, - 1)
The radius of the circle is half of the length of the hypotenuse.
⇒ ![]()
⇒ r3 = 1 units.
We know that the equation of the circle with centre (p, q) and having radius ‘r’ is given by:
⇒ (x - p)2 + (y - q)2 = r2
Now we substitute the corresponding values in the equation to get the circle’s equation for ΔOBC:
⇒ ![]()
⇒ x2 + y2 + 2y + 1 = 1
⇒ x2 + y2 + 2y = 0
⇒ Circumcentre (C4) of OCD = ![]()
⇒ C4 = (- 1,0)
The radius of the circle is half of the length of the hypotenuse.
⇒ ![]()
⇒ r4 = 1 units.
We know that the equation of the circle with centre (p, q) and having radius ‘r’ is given by:
⇒ (x - p)2 + (y - q)2 = r2
Now we substitute the corresponding values in the equation to get the circle’s equation for ΔOAC:
⇒ ![]()
⇒ x2 + 2x + 1 + y2 = 1
⇒ x2 + y2 + 2x = 0
∴The equation of the circles are x2 + y2 - 2x = 0, x2 + y2 - 2y = 0, x2 + y2 + 2y = 0 and x2 + y2 + 2x = 0.