The area of an equilateral triangle inscribed in the circle x 2 + y 2 – 6x – 8y – 25 = 0 is

Question

Philoid · Accepted Answer

We need to find the area of the equilateral triangle that is inscribed in the circle x² + y² - 6x - 8y - 25 = 0.

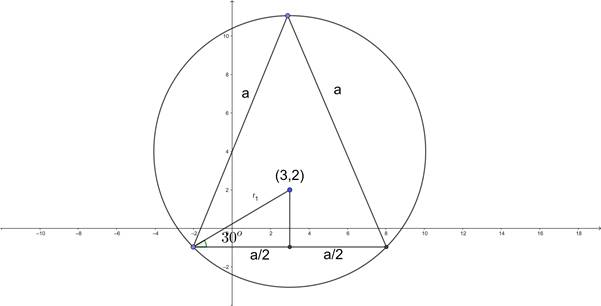
We know that for a circle x² + y² + 2ax + 2by + c = 0

⇒ Centre = (- a, - b)

⇒ Radius =

For x² + y² - 6x - 8y - 25 = 0

⇒ Radius(r₁) =

⇒

From the figure we can see that,

⇒

We know that area of the equilateral triangle with side length ‘a’ is

⇒

⇒ .

∴The correct option is (a).