If SinA = 1/2, cosB = 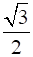 , where π/2<A < π And 0 <B < π/2, find the following:
, where π/2<A < π And 0 <B < π/2, find the following:
(i) tan(A +B)(ii) tan(A -B)
Given sinA = 1/2 And cosB = √3/2 where π/2 <A < π And 0 <B < π/2,
A is in second quadrant And B is in first quadrant.
In the second quadrant, the sine function is positive And cosine And tan functions are negative.
In first quadrant, All functions are positive.
We know that ![]()
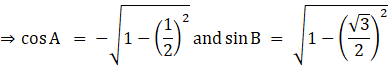
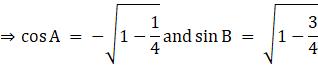
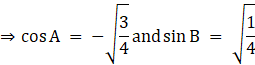
![]()
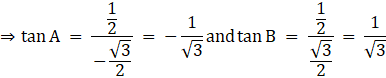
Then,
(i) tan(A +B)
We know that ![]()
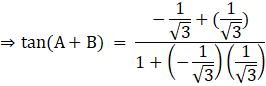
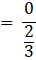
= 0
(ii) tan(A –B)
We know that ![]()
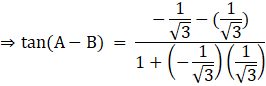
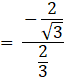
![]()
6