If α,β are two different values of x lying between 0 And 2π which satisfy the equation 6 cos x + 8 sin x = 9, find the value of Sin(α+β).
Given 6 cos x + 8 sin x = 9
Case 1:
⇒ 6 cos x = 9 – 8 sin x
Squaring on both sides,
⇒ 36 cos2 x =(9 – 8 sin x)2
We know that cos2 x = 1 – sin2 x.
⇒ 36(1 – sin2 x) = 81 + 64 sin2 x – 144 sin x
⇒ 100 sin2 x – 144 sin x + 45 = 0
∴ cos α And cos β are the roots of the a bove equation
⇒ sin α sin β = 45/100
Case 2:
⇒ 8 sin x = 9 – 6 cos x
Squaring on both sides,
⇒ 64 sin2 x =(9 – 6 cos x)2
We know that sin2 x = 1 – cos2 x
⇒ 64(1 – cos2 x) = 81 + 36 cos2 x – 108 cos x
⇒ 100 cos2 x – 108 cos x + 17 = 0
∴ sin α And sin β are the roots of theAbove equation
⇒ cos α cos β = 17/100
Consider cos(α + β),
We know that cos(A +B) = cosA cosB - sinA sinB
![]()
We know that ![]()
![]()
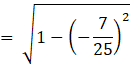
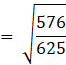
![]()