If sin α + sin β =A And cos α + cos β =B, show that
(i) 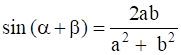
(ii) 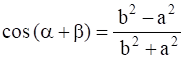
Given sin α + sin β =A And cos α + cos β =B.
⇒A2 +B2 =(sin α + sin β)2 +(cos α + cos β)2
= sin2 α + sin2 β + 2 sin α sin β + cos2 α + cos2 β + 2 cos α cos β
= sin2 α + cos2 α + sin2 β + cos2 β + 2(sin α sin β + cos α cos β)
We know that cos(A -B) = cosA cosB + sinA sinB
∴A2 +B2 = 2 + 2 cos(α – β) …(1)
Then,
⇒B2 –A2 =(cos α + cos β)2 –(sin α + sin β)2
= cos2 α + cos2 β + 2 cos α cos β –(sin2 α + sin2 β + 2 sin α sin β)
=(cos2 α – sin2 β) +(cos2 β – sin2 α) – 2cos(α + β)
= 2 cos(α + β) cos(α – β) + 2 cos(α + β)
= cos(α + β)(2 + 2 cos(α – β)) …(2)
From(1) And(2),
⇒B2 –A2 = cos(α + β)(A2 +B2)
![]() …(ii)
…(ii)
And ![]()
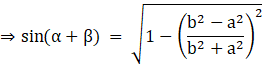
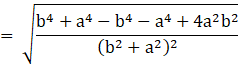
![]() …(i)
…(i)
28