Find the maximum and minimum values of each of the following trigonometrical expressions:
(i) 12 sin x- 5 cos x
(ii) 12 cos x + 5 sin x+ 4
(iii) 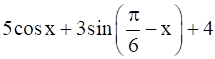
(iv) sin x – cos x + 1
We know that the maximum value of Acosα + Bsinα + c is
c + √(A2 +B2)
And the minimum value is c - √(a2 +B2).
(i) Given f(x) = 12 sin x – 5 cos x
Here A = -5,B = 12 and c = 0
![]()
![]()
![]()
⇒ -13 ≤ 12 sin x - 5 cos x ≤ 13
Hence, the maximum and minimum values of f(x) are 13 and -13 respectively.
(ii) Given f(x) = 12 cos x + 5 sin x + 4
Here A = 12,B = 5 and c = 4
![]()
![]()
![]()
⇒ -9 ≤ 12 cos x + 5 sin x + 4 ≤ 17
Hence, the maximum And minimum values of f(x) are 17 And -9 respectively.
(iii) Given ![]()
We know that sin(A -B) = sinA cosB - cosA sinB
![]()
![]()
![]()
Here ![]()
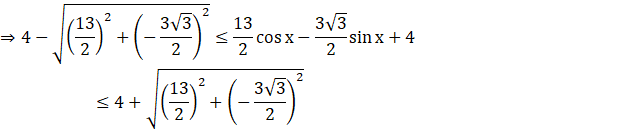
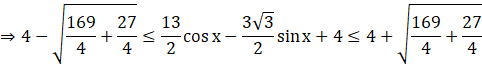
![]()
⇒ -3 ≤ ![]() ≤ 11
≤ 11
Hence, the maximum And minimum values of f(x) are 11 And -3 respectively.
(iv) Given f(x) = sin x – cos x + 1
Here A = -1,B = 1 And c = 1
![]()
![]()
![]()
Hence, the maximum And minimum values of f(x) are ![]() And
And ![]() respectively.
respectively.