find the equation of the ellipse in the following cases:
eccentricity 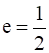 and foci (± 2, 0)
and foci (± 2, 0)
Given that we need to find the equation of the ellipse whose eccentricity is ![]() and foci (±2,0).
and foci (±2,0).
Let us assume the equation of the ellipse as ![]() (a2>b2).
(a2>b2).
We know that eccentricity(e) = ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
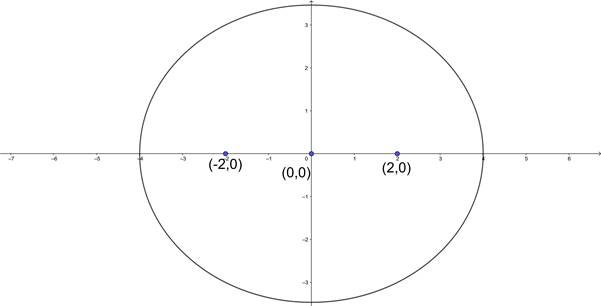
We know that foci = (±ae,0)
⇒ ae = 2
⇒ ![]()
⇒ a = 4
⇒ a2 = 16
⇒ ![]()
⇒ b2 = 12
The equation of the ellipse is
⇒ ![]()
⇒ ![]()
⇒ 3x2 + 4y2 = 48
∴ The equation of the ellipse is 3x2 + 4y2 = 48.
5