Find the equation of an ellipse whose axes lie along the coordinates axes, which passes through the point (- 3, 1) and has eccentricity equal to .

Question

Philoid · Accepted Answer

Given that we need to find the equation of the ellipse whose eccentricity is and passes through (- 3,1).

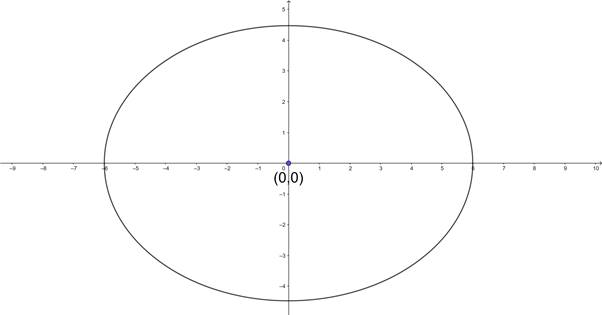
Let us assume the equation of the ellipse is - - - - (1) (a²>b²).

We know that eccentricity of the ellipse is

⇒

⇒ 5a² - 5b² = 2a²

⇒ 5b² = 3a²

⇒ ..... - - - (2)

Substituting the point (- 3,1) in (1) we get,

⇒

⇒ 5b² = 32

⇒

From (2),

⇒

The equation of the ellipse is

⇒

⇒ 3x² + 5y² = 32

∴ The equation of the ellipse is 3x² + 5y² = 32.