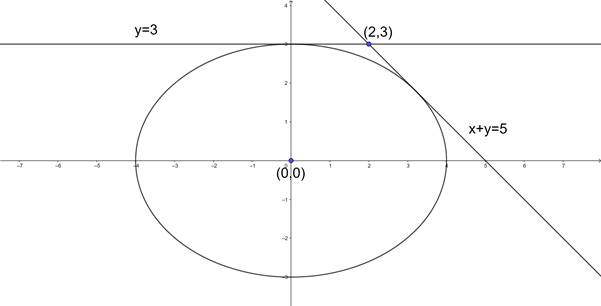
The equations of the tangents to the ellipse 9x2 + 16y2 = 144 from the point (2, 3) are
Given that we need to find the equation of the tangents to the ellipse 9x2 + 16y2 = 144 from the point (2,3).
We know that tangent at any point (x1,y1) on the ellipse is S1 = 0.
⇒ S1 = 0
⇒ 9(xx1) + 16(yy1) = 144 .... (1)
This passes through the point (2,3)
⇒ 9(2x1) + 16(3y1) = 144
⇒ 18x1 + 48y1 = 144
⇒ 3x1 + 8y1 = 24
⇒ 8y1 = 24 - 3x1
⇒ ![]() .... - - (2)
.... - - (2)
Substituting this in the equation of the ellipse we get,
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
From (2)
⇒ ![]()
⇒ y1 = 3
⇒ ![]()
⇒ ![]()
⇒ ![]()
Substituting x1 = 0 and y1 = 3 in (1), we get
⇒ 9(x(0)) + 16(y(3)) = 144
⇒ 48y = 144
⇒ y = 3.
Substituting ![]() and
and ![]() in (1), we get
in (1), we get
⇒ ![]()
⇒ ![]()
⇒ x + y = 5
∴ The correct option is D
10