Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm 3 , which has the minimum surface area?

Question

Philoid · Accepted Answer

Let the radius and height of right circular cylinder be r and h respectively.

Given: Volume of Cylindrical can = 100 cm³

Volume of a cylinder = πr²h

πr²h = 100

… 1

Surface of a cylinder, S = 2πrh + 2πr²

From equation we get,

Condition for maxima and minima

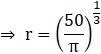
So, for

>0

This is the condition for minima

From equation 1,

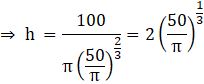
Hence, required dimensions of cylinders are radius = and height =