A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.

Question

Philoid · Accepted Answer

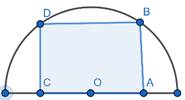
Let the length and breadth of rectangle ABCD be 2x and y respectively

Radius of semicircle = r (given)

In triangle OBA

r² = x² + y² (Pythagoras theorem)

y² = r² - x²

…1

Let us say, area of rectangle = A =xy

A = x () (from equation 1)

Condition for maxima and minima is

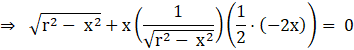
r² – x² = x²

2x² = r²

x =

Since, x cannot be negative

Hence,

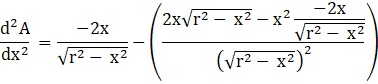
For , < 0

A will be maximum for

From equation 1

y = =

Length of rectangle =

Breadth of rectangle =

Area of rectangle =